The 75 Uniform Compounds of Uniform Polyhedra

In 1976 John Skilling published "Uniform Compounds of Uniform Polyhedra [Ref]. Many, if not all, of these models may have appeared in Michael G. Harman, "Polyhedral Compounds" [Ref], an unpublished manuscript around 1974. However, the concept of Uniform Compounds with Rotational Freedom was first published in Skilling's paper. Historically, at least some of the Uniform Compounds were known. Peter Cromwell notes in his book Polyhedra [Ref] that the compound of two tetrahedra was first depicted in Pacioli's Divina Proportione [Ref] and the compounds of five and ten tetrahedra, of five cubes, and of five octahedra were first described by Edmund Hess [Ref] in 1876.

In 1996, George Hart generated many, but not all of them, as vrml models for the first time. In 2006 Piotr Pawlikowski noticed that there was still no one place where all of the 75 models could be found. With the help of Marcel Tunnissen and others, he completed the missing models for a collection of 75 Stella files. From those, the vrml models could be generated, completing the series. Those models served as the inspiration for this web page.

A Uniform Compound was described by Skilling as "a three-dimensional combination of uniform polyhedra whose edge-lengths are all equal and whose relative position is such that the symmetry group of the combination is transitive on the set of all vertices of the polyhedra. The polyhedra may intersect themselves and each other, but compounds in which some faces are either shared between constituents or totally hidden from exterior view are excluded".

Sometimes erroneously referred to as "vertex uniform", the property of the vertices of the Uniform Compounds is that they are isogonal (literally "same-vertexed"). To be one of the Uniform Compounds, the vertices must be situated in a "kaleidoscopic" pattern such that if a section of it were displayed in 3 mirrors as in a sort of 3D kaleidoscope, and it was carefully rotated it would continue to look like the whole compound. The vertices of a Uniform Compound will also all be identical such that they all have the same valence. But just having vertex congruence within a given geometry is not enough. For instance, 20 cubes can be situated in an icosahedral pattern, but the vertices on their corners are not isogonal. While not instantly apparent, if the kaleidoscope test were done on the vertices, it could be seen as not quite right.

Isogonality and isohedrality are dual properties. Taking the dual of any of the Uniform Compounds, all which have one kind of vertex, will result in a compound with only one kind of face. For instance the dual of the Compound of 4 Hexagonal Prisms will be a compound of 4 Hexagonal Dipyramids and all faces will be triangles of the same shape and size (isohedral). Most of the time even when the dual has faces of regular polygons it is not a Uniform Compound. For instance, while the compound of 20 octahedra is isogonal, its dual is of all the square faces of 20 cubes but again it is not a Uniform Compound because it has two types of vertices. In fact, other than the self-dual tetrahedral compounds, there is only one case such that the dual of a Uniform Compound is also a Uniform Compound. In the case of the Compound of 5 Cubes, its dual, the Compound of 5 Octahedra is also a Uniform Compound.

Some interesting facts about the Uniform Compounds.

• There are 10 chiral compounds on this list - 5, 18,19, 30, 32, 34, 36, 42, 44, 55. In 8 cases (except 18 and 19) the next compound on the list is the compound of left and right hand versions.
  
  
• Number 20 through 26 represent an infinite set. 20, 22 and 24 are compounds of any even number of the constituents. They all have rotational freedom. 20 are compounds of prisms, 22 and 24 antiprisms. The base is n/m polygon - in 22 m is odd (e.g. 5/3, 8/3, etc) and in 24 m is even (5/2, 9/4 etc). 21, 23 and 25 are special cases of the previous with no freedom. They can be compounds of any number of constituents.
  
  
• 50 have Icosahedral Symmetry. 17 have Octahedral Symmetry. Only 2 have Tetrahedral Symmetry. 20 through 26 have Prismatic Symmetry.
  
  
• 12 of the compounds are isohedral, having on one face type. These are 1, 2, 3, 4, 5, 6, 9, 17, 48, 49, 50, and 51. In addition, 22 and 23 qualify if digonal antiprisms are used.
  
  
• 5 of the compounds are regular, being transitive on vertices, faces, and edges. These are 4, 5, 6, 9 and 17. Also 59, 60 and 61 are edge-transitive (so Isotoxal) but have more than one face type.
  
  
• George Hart quips at the bottom of this page that if you ever make a paper model of the Great Retrosnub Icosidodecahedron and its Reflection (72), he will "buy you a beer". So far there are three known paper models of it. One by Jonathan Bowers and the other by Piotr Pawlikowski. George bought Jonathan a root beer since he does not drink beer. Piotr received the promised beer at the Bridges Conference in Pecs (2010). Marcel Tünnissen recently built the model seen here and here (No beer yet, though). Anyone who wants to tackle it can import the stel file into Stella. It requires only 2580 parts!
  
  
• Piotr Pawlikowski has an online galleries of some paper models here, here and here. Of these, the paper model of the Compound of 5 Great Rhombicuboctahedra (67) is thought to be the only one ever attempted requiring over 3500 parts.
  
  
• Please submit anything else you believe should be a bullet item.

Links to other pages for further reading:

• George Hart's Uniform Compounds
• George Hart's Spinning Versions of The Uniform Compounds
• Marcel Tunnissen's Table of The Uniform Compounds
• Jonathan Bowers' Uniform Polychora page (at the bottom). Bowers also provides Uniform Compounds Short Names
• Wikipedia Page on Uniform Compounds

Question or comments about the web page should be directed to PolyhedraSmith@gmail.com

The compounds are presented in the order Skilling originally listed them. The Super Heading of each table is the group name from Skilling's paper for which those compounds belong. Each figure lists the symmetry (S) T - Tetrahedral, O - Octahedral, I - Icosahedral, number of faces of each type - Triangle, Square, Pentagon, Hexagon, Octagon and Decagon. Total Face, Edge and Vertex counts are given such that each compound constituent is a separate entity. A (C) denotes that solid is chiral. An (R) denotes rotational freedom. For Compounds with Rotation Freedom, animations of different aspects of the model are provided.

Links below display various models

• Clicking on pictures opens an Interactive OFF Viewer
• Clicking on Animated GIFS open larger version of Animated GIFS
• Clicking on the title of a model opens a Povray picture of the model
• OFF files open in an online browser. Downloaded files may be viewed with an application such as Antiprism
• STEL files may be saved and opened with Stella
• VRML files (wrl,switch,cyl) open in an online browser. Downloaded files may be viewed with a VRML browser such as FreeWRL

Miscellaneous 1-5
01 - 6 Tetrahedra (R) S 3 4 5 6 8 10 T 24 * * * * * F=24       E=36       V=24 D2v   D2v   D2v   C3v	02 - 12 Tetrahedra (R) S 3 4 5 6 8 10 O 48 * * * * * F=48       E=72       V=48 D4h   D4h   D4h   D3v	03 - 6 Tetrahedra S 3 4 5 6 8 10 O 24 * * * * * F=24       E=36       V=24 off  stel     wrl  switch cyl	04 - 2 Tetrahedra S 3 4 5 6 8 10 I 8 * * * * * F=8       E=12       V=8 off  stel     wrl  switch cyl	05 - 5 Tetrahedra (C) S 3 4 5 6 8 10 I 20 * * * * * F=20       E=30       V=20 off  stel     wrl  switch cyl
Miscellaneous 6-10
06 - 10 Tetrahedra S 3 4 5 6 8 10 I 40 * * * * * F=40       E=60       V=40 off  stel     wrl  switch cyl	07 - 6 Cubes (R) S 3 4 5 6 8 10 O * 36 * * * * F=36       E=72       V=48 D4h   D4h   D4h   D3v	08 - 3 Cubes S 3 4 5 6 8 10 O * 18 * * * * F=18       E=36       V=24 off  stel     wrl  switch cyl	09 - 5 Cubes S 3 4 5 6 8 10 I * 30 * * * * F=30       E=60       V=40 off  stel     wrl  switch cyl	10 - 4 Octahedra (R) S 3 4 5 6 8 10 T 32 * * * * * F=32       E=48       V=24 D2h   D2h   D2h   S6
Miscellaneous 11-15
11 - 8 Octahedra (R) S 3 4 5 6 8 10 O 64 * * * * * F=64       E=96       V=48 D4h   D4h   D4h   D3v	12 - 4 Octahedra S 3 4 5 6 8 10 O 32 * * * * * F=32       E=48       V=24 off  stel     wrl  switch cyl	13 - 20 Octahedra (R) S 3 4 5 6 8 10 I 160 * * * * * F=160       E=240       V=120 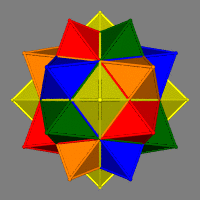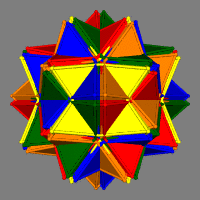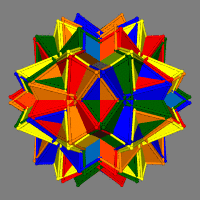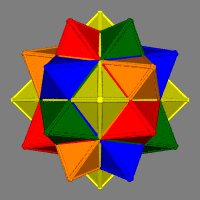D2h   D3v   D5v	14 - 20 Octahedra S 3 4 5 6 8 10 I 160 * * * * * F=160       E=240       V=120 off  stel     wrl  switch cyl	15 - 10 Octahedra S 3 4 5 6 8 10 I 80 * * * * * F=80       E=120       V=60 off  stel     wrl  switch cyl
Miscellaneous 16-19
16 - 10 Octahedra S 3 4 5 6 8 10 I 80 * * * * * F=80       E=120       V=60 off  stel     wrl  switch cyl	17 - 5 Octahedra S 3 4 5 6 8 10 I 40 * * * * * F=40       E=60       V=30 off  stel     wrl  switch cyl	18 - 5 Tetrahemihexahedron (C) S 3 4 5 6 8 10 I 20 15 * * * * F=35       E=60       V=35 off  stel     wrl  switch cyl	19 - 20 Tetrahemihexahedron (C) S 3 4 5 6 8 10 I 80 60 * * * * F=140       E=240       V=140 off  stel     wrl  switch cyl
Prism Symmetry, Embedded in Prism Symmetry 20-24 (Examples)
20 - 2k n-d-gonal prisms (12 Triangular Prisms) (R) D2h   D2h   D18h	21 - k n-d-gonal prisms (6 Triangular Prisms) off   stel   wrl	22 - 2k n-odd-d-gonal antiprisms (8 Digonal Antiprisms) (R) D2h   D2h   D8h	23 - k n-odd-d-gonal antiprisms (4 Digonal Antiprisms) off   stel   wrl	24 - 2k n-even-d-gonal antiprisms (12 Pentagrammic Antiprisms) (R) D2h   D2h   D30h
Prism Symmetry, Embedded in Prism Symmetry 25 (Examples)
25 - k n-even-d-gonal antiprisms (6 Pentagrammic Antiprisms) off   stel   wrl
Prism Symmetry, Embedded in Octahedral or Icosahedral Symmetry 26-30
26 - 12 Pentagonal Antiprisms (R) S 3 4 5 6 8 10 I 120 * 24 * * * F=144       E=240       V=120 D2h   D3v   D5v	27 - 6 Pentagonal Antiprisms S 3 4 5 6 8 10 I 60 * 12 * * * F=72       E=120       V=60 off  stel     wrl  switch cyl	28 - 12 Pentagrammic Crossed Antiprisms (R) S 3 4 5 6 8 10 I 120 * 24 * * * F=144       E=240       V=120 D2h   D3v   D5v	29 - 6 Pentagrammic Crossed Antiprisms S 3 4 5 6 8 10 I 60 * 12 * * * F=72       E=120       V=60 off  stel     wrl  switch cyl	30 - 4 Triangular Prisms (C) S 3 4 5 6 8 10 O 8 12 * * * * F=20       E=36       V=24 off  stel     wrl  switch cyl
Prism Symmetry, Embedded in Octahedral or Icosahedral Symmetry 31-35
31 - 8 Triangular Prisms S 3 4 5 6 8 10 O 16 24 * * * * F=40       E=72       V=48 off  stel     wrl  switch cyl	32 - 10 Triangular Prisms (C) S 3 4 5 6 8 10 I 20 30 * * * * F=50       E=90       V=60 off  stel     wrl  switch cyl	33 - 20 Triangular Prisms S 3 4 5 6 8 10 I 40 60 * * * * F=100       E=180       V=120 off  stel     wrl  switch cyl	34 - 6 Pentagonal Prisms (C) S 3 4 5 6 8 10 I * 30 12 * * * F=42       E=90       V=60 off  stel     wrl  switch cyl	35 - 12 Pentagonal Prisms S 3 4 5 6 8 10 I * 60 24 * * * F=84       E=180       V=120 off  stel     wrl  switch cyl
Prism Symmetry, Embedded in Octahedral or Icosahedral Symmetry 36-40
36 - 6 Pentagrammic Prisms (C) S 3 4 5 6 8 10 I * 30 12 * * * F=42       E=90       V=60 off  stel     wrl  switch cyl	37 - 12 Pentagrammic Prisms S 3 4 5 6 8 10 I * 60 24 * * * F=84       E=180       V=120 off  stel     wrl  switch cyl	38 - 4 Hexagonal Prisms S 3 4 5 6 8 10 O * 24 * 8 * * F=32       E=72       V=48 off  stel     wrl  switch cyl	39 - 10 Hexagonal Prisms S 3 4 5 6 8 10 I * 60 * 20 * * F=80       E=180       V=120 off  stel     wrl  switch cyl	40 - 6 Decagonal Prisms S 3 4 5 6 8 10 I * 60 * * * 12 F=72       E=180       V=120 off  stel     wrl  switch cyl
Prism Symmetry, Embedded in Octahedral or Icosahedral Symmetry 41-45
41 - 6 Decagrammic Prisms S 3 4 5 6 8 10 I * 60 * * * 12 F=72       E=180       V=120 off  stel     wrl  switch cyl	42 - 3 Square Antiprisms (C) S 3 4 5 6 8 10 O 24 6 * * * * F=30       E=48       V=24 off  stel     wrl  switch cyl	43 - 6 Square Antiprisms S 3 4 5 6 8 10 O 48 12 * * * * F=60       E=96       V=48 off  stel     wrl  switch cyl	44 - 6 Pentagrammic Antiprisms (C) S 3 4 5 6 8 10 I 60 * 12 * * * F=72       E=120       V=60 off  stel     wrl  switch cyl	45 - 12 Pentagrammic Antiprisms S 3 4 5 6 8 10 I 120 * 24 * * * F=144       E=240       V=120 off  stel     wrl  switch cyl
Tetrahedral Symmetry, Embedded in Octahedral or Icosahedral Symmetry 46-50
46 - 2 Icosahedra S 3 4 5 6 8 10 O 40 * * * * * F=40       E=60       V=24 off  stel     wrl  switch cyl	47 - 5 Icosahedra S 3 4 5 6 8 10 I 100 * * * * * F=100       E=150       V=60 off  stel     wrl  switch cyl	48 - 2 Great Dodecahedra S 3 4 5 6 8 10 O * * 24 * * * F=24       E=24       V=60 off  stel     wrl  switch cyl	49 - 5 Great Dodecahedra S 3 4 5 6 8 10 I * * 60 * * * F=60       E=60       V=150 off  stel     wrl  switch cyl	50 - 2 Small Stellated Dodecahedra S 3 4 5 6 8 10 O * * 24 * * * F=24       E=24       V=60 off  stel     wrl  switch cyl
Tetrahedral Symmetry, Embedded in Octahedral or Icosahedral Symmetry 51-55
51 - 5 Small Stellated Dodecahedra S 3 4 5 6 8 10 I * * 60 * * * F=60       E=60       V=150 off  stel     wrl  switch cyl	52 - 2 Great Icosahedra S 3 4 5 6 8 10 O 40 * * * * * F=40       E=60       V=24 off  stel     wrl  switch cyl	53 - 5 Great Icosahedra S 3 4 5 6 8 10 I 100 * * * * * F=100       E=150       V=60 off  stel     wrl  switch cyl	54 - 2 Truncated Tetrahedra S 3 4 5 6 8 10 O 8 * * 8 * * F=16       E=36       V=24 off  stel     wrl  switch cyl	55 - 5 Truncated Tetrahedra (C) S 3 4 5 6 8 10 I 20 * * 20 * * F=40       E=90       V=60 off  stel     wrl  switch cyl
Tetrahedral Symmetry, Embedded in Octahedral or Icosahedral Symmetry 56-60
56 - 10 Truncated Tetrahedra S 3 4 5 6 8 10 I 40 * * 40 * * F=80       E=180       V=120 off  stel     wrl  switch cyl	57 - 5 Truncated Cubes S 3 4 5 6 8 10 I 40 * * * 30 * F=70       E=180       V=120 off  stel     wrl  switch cyl	58 - 5 Quasitruncated Hexahedra S 3 4 5 6 8 10 I 40 * * * 30 * F=70       E=180       V=120 off  stel     wrl  switch cyl	59 - 5 Cuboctahedra S 3 4 5 6 8 10 I 40 30 * * * * F=70       E=120       V=60 off  stel     wrl  switch cyl	60 - 5 Cubohemioctahedra S 3 4 5 6 8 10 I * 30 * 20 * * F=50       E=120       V=80 off  stel     wrl  switch cyl
Tetrahedral Symmetry, Embedded in Octahedral or Icosahedral Symmetry 61-65
61 - 5 Octahemioctahedra S 3 4 5 6 8 10 I 40 * * 20 * * F=60       E=60       V=120 off  stel     wrl  switch cyl	62 - 5 Rhombicuboctahedra S 3 4 5 6 8 10 I 40 90 * * * * F=130       E=240       V=120 off  stel     wrl  switch cyl	63 - 5 Small Rhombihexahedra S 3 4 5 6 8 10 I * 60 * * 30 * F=90       E=120       V=240 off  stel     wrl  switch cyl	64 - 5 Small Cubicuboctahedra S 3 4 5 6 8 10 I 40 30 * * 30 * F=100       E=120       V=240 off  stel     wrl  switch cyl	65 - 5 Great Cubicuboctahedra S 3 4 5 6 8 10 I 40 30 * * 30 * F=100       E=120       V=240 off  stel     wrl  switch cyl
Tetrahedral Symmetry, Embedded in Octahedral or Icosahedral Symmetry 66-67
66 - 5 Great Rhombihexahedra S 3 4 5 6 8 10 I * 60 * * 30 * F=90       E=120       V=240 off  stel     wrl  switch cyl	67 - 5 Great Rhombicuboctahedra S 3 4 5 6 8 10 I 40 90 * * * * F=130       E=120       V=240 off  stel     wrl  switch cyl
Duplication of Enantiomorphs 68-72
68 - 2 Snub Cubes S 3 4 5 6 8 10 O 64 12 * * * * F=76       E=120       V=48 off  stel     wrl  switch cyl	69 - 2 Snub Dodecahedra S 3 4 5 6 8 10 I 160 * 24 * * * F=184       E=300       V=120 off  stel     wrl  switch cyl	70 - 2 Great Snub Icosidodecahedra S 3 4 5 6 8 10 I 160 * 24 * * * F=184       E=300       V=120 off  stel     wrl  switch cyl	71 - 2 Great Inverted Snub Icosidodecahedra S 3 4 5 6 8 10 I 160 * 24 * * * F=184       E=300       V=120 off  stel     wrl  switch cyl	72 - 2 Great Retrosnub Icosidodecahedra S 3 4 5 6 8 10 I 160 * 24 * * * F=184       E=300       V=120 off  stel     wrl  switch cyl
Duplication of Enantiomorphs 73-75
73 - 2 Snub Dodecadodecahedra S 3 4 5 6 8 10 I 120 * 48 * * * F=168       E=120       V=300 off  stel     wrl  switch cyl	74 - 2 Inverted Snub Dodecadodecahedra S 3 4 5 6 8 10 I 120 * 48 * * * F=168       E=120       V=300 off  stel     wrl  switch cyl	75 - 2 Snub Icosidodecadodecahedra S 3 4 5 6 8 10 I 160 * 48 * * * F=208       E=144       V=360 off  stel     wrl  switch cyl

Question or comments about the web page should be directed to PolyhedraSmith@gmail.com.

Thanks to Guy Inchbald for a description of isogonality of Uniform Compound vertices

Generation of VRML models, OFF files, and Pictures was done with Antiprism. Stel were generated with Robert Webb's Stella application. The Hedron application by Jim McNeill was used to generate switch files.

I'd also like to thank Alex Doskey for his spreadsheet method which made the construction of this page much easier. I also use JovoToys in polyhedra contruction.

History:

2024-06-17 Use base.css
2024-06-13 Switch to Multi OFF Viewer
2023-09-03 Switch to Simple OFF Viewer and X_Ite VRML Viewer
2023-06-26 Change mention from Contona to FreeWRL 2019-03-16 Click on pictures goes to live model
2019-03-15 Marcel Tünnissen's gidrissid added
2019-03-12 Changed email address from defunct bigfoot.com
2012-02-22 Rebuilt page
2009-01-30 Update site for Piotr Pawlikowski picture gallery
2008-01-16 Edited part count for 5 Querco
2008-01-07 Added Piotr Pawlikowski picture gallery. Added Wikipedia link. Listed isogonal cases. Clarified isogonality paragraph
2008-01-06 Updated the beer statistics. Added Pictures of gidrissid paper models. Better explanation of "isogonality"
2008-01-05 Added OFF files. Took spaces out of file names
2006-12-21 Cylinder Files added. Big Pictures added
2006-12-16 Jonathan Bowers's site added. #62 Stel file corrected
2006-12-15 70 and 74 untangled
2006-12-13 #67 Face count corrected
2006-12-10 Initial Release
2006-12-03 Beta
2006-12-01 Alpha

Roger's Polyhedra, (c) 2006-2024, Roger Kaufman